4.b.2. Curvatura da luz do efeito das lentes gravitacionais
A predição sobre o comportamento das estrelas como lentes gravitacionais na curvatura da luz é a primeira das famosas três predições da Relatividade Geral de Einstein e foi muito famosa pelo atraso na sua confirmação experimental até ao eclipse solar de 1919.
Também influencia a fama desta predição o fato de supor um efeito de lupa gravitacional simples de visualizar e que a curvatura da luz vaticinada pelo efeito de lente gravitacional, e confirmada era precisamente o dobro da que resultaria de aplicar a Lei de Gravitação Universal de Newton.
É curioso que o continuum espaço-tempo se estique-dilate na curvatura da luz pelo efeito de lentes gravitacionais no fator *2* em relação ao previsto pela Lei de Gravitação de Newton e ninguém pareça saber qual é a razão física, sobretudo porque o número é bastante redondo e simples. Claro, a remissão é sistemática às equações de campo de Einstein, mas nada mais.
Procurando na Internet –ver artigo bending Light en mathpages.com *– ou perguntando a qualquer amigo que de verdade saiba algo de matemática e geometria elíptica, este dirá que uma partícula que passa próximo do Sol descreve uma hipérbole porque este atua como lente gravitacional e que, em função da sua excentricidade, para valores muito pequenos de m em relação a r0e segundo a Lei de Gravitação de Newton, o ângulo ou curvatura total da luz seria igual a:
α = 2 m /r0 = 0,875'' de arco
Então m são a massa do Sol em unidades geométricas –a massa multiplicada por G ou constante de gravitação e dividida pela velocidade da luz ao quadrado– e r0 a distância mais próxima do raio de luz ao Sol.
Recordando um pouco a geometria de um círculo, uma volta inteira tem 360º graus, cada grau tem 60’ minutos e cada minuto 60’’ segundos de arco.
Portanto, o ângulo ou curvatura da luz que provocariam as lentes gravitacionais na Lei da Gravitação Universal de Newton é diretamente proporcional à massa que cria o campo de gravidade, ao ser a força centrípeta diretamente proporcional à massa.
Ainda que um planeta tenha massa, em Mecânica Clássica não se tem em conta essa massa, visto que exerce uma força gravitacional sobre o planeta em função da sua massa gravitacional; mas a força por unidade de massa gravitacional permanecerá constante inclusivamente se se tivesse em conta a massa cinética segundo a Teoria da Relatividade de Einstein – massa equivalência à energia cinética.
Agora, com a Lei da Gravidade Global há uma força adicional, a segunda componente da atractis causa ou efeito Merlin deve-se à velocidade e opera sobre a massa cinética. A massa global é a massa em repouso mais a massa equivalente à energia cinética. No caso da luz a massa em repouso não existe.
No apartado da Lei da Gravidade Global deste livro comentou-se que essa lei deveria estar expressa em termos de energia e não de massa, visto que a interação gravitacional se produz por transferência entre a energia do campo de gravidade e a energia elástica em forma de massa, massa cinética ou diretamente a energia eletromagnética.
Para calcular a curvatura da luz no efeito de lentes gravitacionais sobre a energia eletromagnética, apenas nos resta verificar que a segunda componente ou força de gravidade adicional derivada da velocidade é igual quantitativamente igual a primeira componente.
No caso da energia eletromagnética é simples intuitivamente, visto que o valor da energia cinética da luz será igual à energia cinética equivalente à suposta massa equivalente.
(Imagem de domínio público)

A partir de outra perspectiva, se a primeira componente da atractis causa se deve à velocidade da propagação da tensão longitudinal do Éter Global e esta é igual à velocidade da luz, como a segunda componente ou efeito Merlin se deve à velocidade da luz para o caso da energia eletromagnética; as duas componentes da atractis causa terão o mesmo valor e a curvatura da luz pelas lentes gravitacionais será o dobro da que obteríamos com a Lei de Gravitação de Newton.
A explicação anterior da causa física do efeito de lentes gravitacionais ou curvatura da luz é um resumo do que comentamos no apartado segundo deste livro, e sobre no apartados sobre o movimento com simetria total e com simetria radial da gravidade no livro da Física e Dinâmica Global.
Não obstante, para os que gostam de matemática inclui-se a seguinte análise quantitativa que, para além de ter certo valor educativo, é de alguma maneira, comum à Física Global e à Teoria da Relatividade.
ANÁLISE QUANTITATIVA
Já comentei que o conceito de massa relativista ou o aumento da massa com a velocidade é um aspecto parcialmente correto da Teoria da Relatividade –se se introduz o sistema de referência natural para a velocidade física– e, consequentemente, mantém-se na Física Global; baseado neste último modelo na pura observação experimental e os mecanismos da transferência energética da interação gravitacional, em contraposição à imposição de axiomas matemática à Física.
Dito de outra forma, não é necessário manter a Teoria da Relatividade para aceitar o citado aumento da massa física com a velocidade.
A conhecida fórmula da massa global que serve para deduzir a energia cinética em termos relativistas é a seguinte:
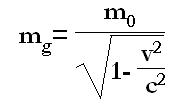
massa global = massa em repouso + massa cinética
[2.a] m = m0 /(1 - v²/c²)½
Ou para breve,
m = γ m0
Como afirmado na Teoria da Relatividade de Einstein, a energia cinética é equivalente ao aumento da massa de repouso m0
O desenvolvimento em série do teorema de Taylor da constante γ dá-nos:
γ = 1+½ v²/c² +3/8 v4/c4 +5/16 v6/c6+...
Energia cinética = m0 [ ½ v²/c² +3/8 v4/c4+5/16 v6/c6+...]
Para este efeito a equação relevante da massa global não deve conter a simplificação realizada para a energia cinética clássica no desenvolvimento em série do teorema de Taylor, uma vez que o segundo termo do parêntesis se torna significativo para velocidades da ordem da luz.
Como bom Einsoutro, perguntei a um amigo mensista, que estava estudando ciências exatas na universidade, e respondeu-me que ele não calculava derivadas terceiras, eu compreendo-o e continua a ser seu amigo.
À margem de episódios simpáticos, no desenvolvimento em série do teorema Taylor só são válidos nos termos correspondentes às derivadas da função simples e quando essas derivadas existam, isto é, sejam distintas de zero. Em geral, matematicamente na igualdade anterior calcula-se o último termo válido de forma a que reúna os termos eliminados.
No nosso caso, se acumulamos ( 1/8v4/c4 ) ao segundo termo recolheremos o efeito residual do resto de termos eliminados e ficaremos com:
Energia cinética = m0 [½v²/c²+½v4/c4]
Logicamente o primeiro termo do parêntesis pode desprezar-se para velocidades baixas ou não planetárias, enquanto que o segundo termo se poderá desprezar para planetárias, mas não para velocidades de ordem próxima ao caso da curvatura da luz e muito menos para a velocidade semelhante ao efeito de lentes gravitacionais. Conseguintemente, numa análise geral hão-se ter-se em conta todas as possibilidades do valor da velocidade da massa física para determinar a força de gravidade total.
(Velocidades próximas da luz)
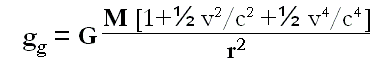
Por esta razão, na equação (2) da página em inglês de Mathpages.com sobre a inércia da energia temos a utilização deste mesmo desenvolvimento em série do teorema de Taylor.
A demonstração da Relatividade Geral de que o efeito das lentes gravitacionais é duplo em relação à Lei de Gravitação de Newton é bastante complicadinha; mas parece que inevitavelmente também se utiliza o mesmo desenvolvimento em série do teorema de Taylor, como se pode ver na página sobre a curvatura da luz do sítio de Mathpages.com citado anteriormente.
Pelo contrário, sem contar o desenvolvimento em série de Taylor, na Física Global, o cálculo não pode ser mais simples.
Logo, o ângulo da curvatura da luz pelo efeito das lentes gravitacionais será o dobro do que prediz a Lei de Gravitação Universal da teoria de Newton. Como já sabíamos pelas famosas observações do eclipse do Sol de 1919 e posteriores, sendo 1,75'' de arco.
