4.b.3. Relatividad de Einstein y la órbita del planeta Mercurio
Si la predicción de la Relatividad General de Einstein sobre la curvatura de la luz es la más llamativa y espectacular por su forma de verificación con la observación del eclipse de 1919, la explicación de la precesión anómala del perihelio de Mercurio –desviación respecto a la Mecánica Celeste de Newton– es la más efectiva por su aspecto cuantitativo.
No obstante, hay que señalar que en 1898 Paul Gerber explicó con anterioridad a la física relativista dicha precesión con una fórmula exactamente igual a la de Einstein.

Los astrónomos habían observado una desviación respecto a la Mecánica Celeste de Newton no explicada por ningún factor conocido de 43,1'' de arco en 100 años en el eje de la órbita del planeta Mercurio, esta desviación de la órbita es a la que me voy a referir como precesión del perihelio de Mercurio, precesión de la órbita de Mercurio o precesión de Mercurio, a pesar de que en sentido estricto la precesión total o suma de la precesión explicada y la no explicada sea bastante mayor. Si se calcula en grados al año la precesión no explicada, resulta en números redondos una diezmilésima de grado al año.
Mediante las tremendamente complejas ecuaciones de campo de la mecánica relativista, Einstein llegó a una cifra muy próxima a los 43'' segundos de arco de precesión de la citada órbita de Mercurio. –Ver la página de mathpages* sobre la explicación de la Relatividad General de la precesión anómala de la órbita de Mercurio.
No es de extrañar que ante el ajuste de las órbitas de los planetas conseguido por la Relatividad General se acabase aceptando la relatividad en su conjunto, en menoscabo de otras alternativas menos aventuradas. Es indudable que las ecuaciones de la Relatividad General de Einstein contienen algunas reglas válidas de comportamiento de la naturaleza aunque estén enmascaradas en sus mecanismos de actuación y de cálculo, como las ideas de Paul Gerber.
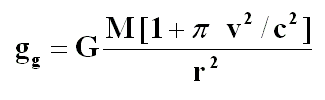
Veamos ahora si las Leyes de la Gravedad Global también explican la precesión del perihelio de Mercurio.
La expresión de la aceleración de la gravedad de la fórmula aportada por la Ley de la Gravedad Global nos da directamente los resultados buscados sobre la desviación angular y la componente normal de la aceleración o aceleración centrípeta.
Para conocer la desviación angular total en una vuelta u órbita de Mercurio lo único que tenemos que hacer es sustituir las variables por sus valores; teniendo en cuenta que la aceleración gg deberá representar la aceleración centrípeta debida tanto a la fuerza de la gravedad correspondiente a la ley de Newton como al efecto Merlín o segunda componente de la atractis causa añadida por las Leyes de la Gravedad Global.
Es decir, gg será la componente normal de la aceleración o aceleración centrípeta que provocará una vuelta completa a la órbita del planeta más la precesión observada para el periodo T.
Este periodo T, por su definición en trigonometría, ocasionaría exactamente una vuelta completa si se considerara exclusivamente la Ley de la Gravitación Universal de Newton, puesto que sabemos que una elíptica perfecta sería consecuencia de la ley del inverso del cuadrado del radio; como se observa en las leyes de Kepler deducidas de las órbitas de los planetas de la Mecánica Celeste.
La vía rápida de calcular la aceleración centrípeta o componente normal de la aceleración me la enseño Don Magufo en una pequeña práctica de matemáticas intuitivas. Pero antes de seguir voy a reseñar los datos necesarios para efectuar los cálculos más el innecesario v, que son:
G = constante de gravitación universal = 6,67266 * 10-11 (m² N / kg²)
c = velocidad de la luz = 2,99792458 * 108 (m/s)
M = Masa del Sol = 1,98892 * 1030 (Kg.)
r = radio medio de órbita de Mercurio = 57,9 * 106 (m)
T = período órbita de Mercurio = 7,60018 * 106 segundos = 414,9378 órbitas en 100 años.
v = velocidad media de Mercurio = 47948,31 (m/s)
Para la comprobación empírica de la fórmula de la dinámica del planeta Mercurio se ha seguido los siguientes pasos:
Simplificación al caso de órbita planetaria circular.
Se ha considerado el caso de una órbita circular del planeta para simplificar los cálculos, porque el juego de fuerzas de la gravedad seguiría existiendo y la excentricidad de la órbita del planeta Mercurio es bastante baja. Desde luego es suficiente para mi propósito aquí.
Cálculo de las vueltas por periodo con la Ley de la Gravedad de Newton.
La fórmula de la Ley de la Gravedad Global se puede escribir con sus dos componentes:
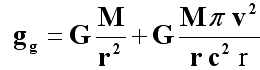
Donde el primer término de la parte derecha es la fórmula correspondiente a la Ley de la Gravitación Universal de Newton o aceleración centrípeta. La variación angular producida por la misma en un periodo debería ser, en principio, igual a una vuelta o 2π radianes.
Entonces, si lo multiplicamos y lo dividimos por v² y sustituimos v²/r por la componente normal de la aceleración o aceleración centrípeta an nos quedará:
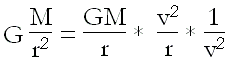
Y recordando que el valor de la velocidad orbital es la raíz cuadrada de GM/r tenemos que:
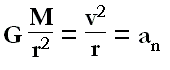
v T = 2πr
w T = 2π
v / r = w
an / v = w
an T / v = T (v²/r) (1/v)
= Tv/r = wT =
= 2π Radianes Q.E.D.
Como la componente normal de la aceleración an está relacionada con el cambio de la dirección de la velocidad con el tiempo, si calculamos dicho cambio por cada m/s (dividiéndola por v) y la multiplicamos por el período T o número de segundos totales en una vuelta nos dará por trigonometría 2π radianes o una vuelta entera de la órbita del planeta Mercurio o cualquier otro planeta o astro de la Mecánica Celeste.
Lo anterior se puede comprobar efectuando los cálculos utilizando el valor de la velocidad media del planeta Mercurio. –Una vuelta entera tiene 2π radianes o 360º grados, cada grado tiene 60' minutos y cada minuto 60'' segundos de arco.
Aceleración centrípeta
y velocidad lineal del planeta MercurioG 6,67266E-11 Masa del Sol 1,98892E+30 GM 1,32714E+20 Radio medio órbita 5,79000E+10 an= GM/r² 3,95876E-02 v media Mercurio 4,794831E+4 an / v = w 8,25631E-07 Vueltas 100 años 4,149378E+02 Periodo T de la órbita 7,60018E+06 w * T = 2 π 6,27494E+00 Cálculo de las vueltas por periodo debidas al efecto Merlín.
Lo que nos interesa de verdad es el segundo componente de la fórmula de la Ley de la Gravedad Global; puesto que será la aceleración centrípeta provocada por el efecto Merlín –por la doble atracción debida a la energía cinética. Dicha aceleración centrípeta ocasionará la precesión del perihelio de Mercurio (ppm) –o de la órbita de cualquier planeta en la Mecánica Celeste–, si la calculamos para todo el período considerado como hemos hecho anteriormente con a(n) para calcular los 2π radianes.
Según Don Magufo se puede resolver directamente la integral intuitiva de la ecuación diferencial no planteada si, una vez sustituido v²/r por an, ponemos su valor para un periodo entero; que como acabamos de discutir más arriba en términos de trigonometría y geometría del círculo será 2π.
La integral formal respecto al periodo de tiempo de la aceleración centrípeta o normal se resuelve sin ningún problema; pues tanto la velocidad, la aceleración centrípeta y el resto de variables son constantes o independientes del tiempo por la simplificación a una órbita circular del planeta Mercurio. Por ello, coincide con los cálculos básicos de trigonometría pues la integral de *dt* es 1.
Así, quedará que en:
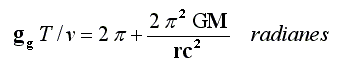
Por lo tanto, la precesión del perihelio de Mercurio en radianes será:

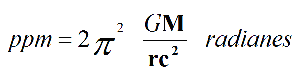
El valor de la ppm obtenido con la igualdad anterior, derivada de la Física Global es de43,08'' segundos de arco cada 100 años como se muestra en la siguiente tabla:
Cálculo de la precesión del perihelio de Mercurio G 6,67266E-11 Masa del Sol 1,98892E+30 GM 1,32714E+20 Radio medio órbita 5,79000E+10 an= GM/r 2,29212E+09 c² 8,98755E+16 GM / r c² 2,55033E-08 π 3,141592654 π GM / r c² 8,01210E-08 2 π Radianes/vuelta 6,283185307 ppm = 2π² GM / r c² 5,03415E-07 Vueltas/100 años 4,14938E+02 radianes/100 años 2,08886E-04 Segundos/radian 2,06265E+05 seg. arco/100 years 4,30858E+01 * * *
Recordemos que si en esta fórmula cambiásemos 2π por 6 nos daría la fórmula obtenida por Paul Gerber 1898 y Einstein en la Relatividad General con independencia de la excentricidad, como se menciona en libro de la Teoría de la Relatividad, Elementos y Crítica.
Para la Tierra la relatividad general da un valor de 3,8 segundos de arco, la Física Global de 4,02 y el valor observado está en 5 segundos de arco según la página en Internet de Matpages citada anteriormente.
Aunque no cabe duda que ambas teorías son dos buenas aproximaciones –tres si incluimos a Paul Gerber– o formas de ver lo mismo en relación a la órbita del planeta Mercurio, hay que dejar claro que ambas son incompatibles entre sí, pues se explicaría doblemente la misma desviación angular.
| Radio medio 106 km |
Planetas | Radianes | Vueltas 100 años |
Total radianes | Precesión segundos de arco | ||
|---|---|---|---|---|---|---|---|
| Observado | RG | FG | |||||
| 57,90 | Mercurio | 5,03415E-07 | 414,93780 | 2,08886E-04 | 43.10 | 42,9195 | 43,08581 |
| 108,20 | Venus | 2,69387E-07 | 162,60160 | 4,38028E-05 | 8.65 | 8,6186 | 9,03498 |
| 149,60 | Tierra | 1,94838E-07 | 100,00000 | 1,94838E-05 | 3,85 | 3,8345 | 4,01882 |
| 227,90 | Marte | 1,27897E-07 | 53,19150 | 6,80303E-06 | 1,36 | 1,3502 | 1,40323 |
| 778,30 | Júpiter | 3,74505E-08 | 8,43170 | 3,15771E-07 | 0,0623 | 0,06513 | |
| 1427,00 | Saturno | 2,04259E-08 | 3,39440 | 6,93336E-08 | 0,0137 | 0,01430 | |
| 2869,60 | Urano | 1,01574E-08 | 1,19030 | 1,20904E-08 | 0,0024 | 0,00249 | |
| 4496,60 | Neptuno | 6,48217E-09 | 0,60680 | 3,93338E-09 | 0,0008 | 0,00081 | |
| 5900,00 | Plutón | 4,94029E-09 | 0,40320 | 1,99193E-09 | 0,0004 | 0,00041 | |
Además, se basan en principios diferentes y contradictorios; lo que hará que no haga falta recurrir a la navaja de Occam, ya que existen otros fenómenos naturales o experimentos de física que ayudarán a inclinar la balanza de forma definitiva.
Con las Leyes de la Gravedad Global, hemos verificado que se explica exactamente la precesión del perihelio de Mercurio, como consecuencia del efecto Merlín en la interacción del Éter Global (gravitacional - cinético - masa) con los cuerpos con masa.
En otras palabras, el principio de igualdad entre masa gravitatoria y masa inercial establecido por Newton y mantenido por Einstein es impreciso e innecesario, puesto que el comportamiento de la masa física en su interacción con el Éter Global es el mismo, tanto si se estudia con o sin campo gravitatorio; si bien, las fuerzas actuantes son distintas.
En el apartado sobre la Segunda Ley de Newton o Ley de la Fuerza del libro Física y Dinámica Global se detallan las diferencias entre la concepción de Newton, de Einstein y de la propia Física Global debidas a cambios intrínsecos en la masa y en las fuerzas actuantes.
Otros experimentos relacionados con las órbitas planetarias se encuentran en las páginas sobre la sonda Gravity Probe-B de este mismo libro y la Paradoja del último delfín relativista del libro de Astrofísica y Cosmología Global.
Finalmente, quiero remarcar que en ningún momento se ha abandonado la geometría no curvada del espacio euclidiano, a pesar de la órbita del planeta Mercurio, y que la Física Global es consistente con un tiempo absoluto.
Cuando Einsotro acabó la página Web,
va tan contento a decírselo a Pollwick y éste le dice:
–Muy bien. ¿Y qué hiciste después?–
Einsotro, dudando un pico, le dijo:
–Me puse a jugar con mis canicas
y a pensar en el número π.
Entonces apareció una niña pija,
se tiró a mis pies,
y se abrió de pier...
mirando fijamente a mis pibolitas.–
Y Pollwick comentó:
–¡Qué picursi!–
