3.b.3. La energía mecánica
En la Física Moderna, la definición de la energía mecánica es la suma de las energías cinética y potencial asociadas a una masa en un campo gravitatorio. En ausencia de otras fuerzas la energía mecánica de un cuerpo en órbita se mantiene constante.
La energía mecánica es un concepto abstracto de suma de energías de naturaleza matemática, que enlaza o relaciona las causas del movimiento inercial con el movimiento debido a la fuerza de la gravedad.
La razón de que la energía mecánica sea constante es convencional o derivada de principio de conservación de la energía. Si el sistema es cerrado y sólo se contemplan dos manifestaciones de la energía, la suma de ambas ha de ser constante.
Con la teoría de gravitación de Newton se explicaban las órbitas de los planetas y se mantiene el principio de igualdad entre masa inercial y masa gravitatoria. La masa en ambos casos era una constante de proporcionalidad entre la fuerza aplicada y la aceleración resultante de los cuerpos. La aceleración de la gravedad sigue la ley de inverso de los cuadrados.
La Relatividad General de Einstein mantiene el principio de igualdad entre masa inercial y masa gravitatoria, pero sigue sin saber lo que es la masa más allá de una constante de proporcionalidad. La masa no aumenta con la velocidad relativa debido al modelo matemático utilizado, pero se multiplica por γ –de hecho, como si aumentara–, y dicho aumento hace necesaria mayor fuerza a mayor velocidad para producir la misma aceleración.

En la Relatividad General la energía mecánica es mayor que en la Física Clásica de Newton, pues la Energía cinética de un objeto en caída libre vertical será mayor debido al aumento de masa con la velocidad.
Por otra parte, por las observaciones de la Astronomía, la masa gravitatoria parece tener un comportamiento diferente a la masa inercial, y puesto que un aumento de la masa con la velocidad no altera la fuerza de gravitación por unidad de masa, la Relatividad General de Einstein necesita distorsionar el espacio para poder cuadrar las órbitas de los planetas y su precesión anómala respecto de la Ley de Gravitación Universal de Newton.
Un problema adicional creado por la Relatividad General es que, al seguir la distorsión del espacio la misma ley del inverso de los cuadrados, la gravedad entera pasa a ser un efecto geométrico del continuum matemático y se pierden todavía más los conceptos intuitivos de la realidad física.
Puesto que la ley que gobierna la elasticidad del Éter Global está presente en todo tipo de relaciones físicas –como la ley de inverso de los cuadrados–, en muchas ocasiones los cálculos matemáticos de modelos imaginarios son útiles con interpretaciones físicas bastante alejadas de la realidad. Hasta parece que el tema es tan fácil, tan fácil que es fácil confundirse.
Para la Mecánica Global la masa está formada por rizos de los filamentos del Éter Global, gravitacional o cinético. Así, el principio de igualdad de la masa inercial y la masa gravitatoria además de impreciso deja de ser necesario, ya que la masa se define por su realidad física y no por su comportamiento.
En la Física Global, el concepto de energía cinética es una propiedad de la masa asociada a la tendencia de conservar su estado de movimiento, y que implica una mayor resonancia de la masa para mantener la sincronización con la vibración del Éter Global o cinético.
Definición de la energía potencial como propiedad de una masa por encontrarse en un punto de la estructura reticular de la materia –gravitacional o global– con simetría radial.
La Ley de la Gravedad Global aporta una segunda modificación o matización a la Segunda Ley de Newton, Ley de la Fuerza o Ley Fundamental de la Dinámica. Si Einstein introdujo una variación intrínseca de la masa con la velocidad y el correspondiente incremento de atracción gravitatoria más la distorsión del espacio-tiempo, la Ley de la Gravedad Global añade una variación adicional de la fuerza de gravedad debida a la velocidad y distinta de la inducida por el correspondiente incremento de la masa; a pesar de ser ambas variaciones idénticas en términos cuantitativos.
En este caso se producirá un incremento de la aceleración gravitatoria, que dependerá de la energía cinética –en concreto de la relación entre masa cinética y la masa global–, como se observa en la Ley de la Gravedad Global. Esta modificación a la Ley de la Gravitación Universal explica la precesión anómala de las órbitas de los planetas sin alterar el espacio-tiempo.
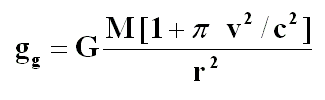
En consecuencia, el nuevo aumento de la fuerza de la gravedad producirá mayor aceleración, mayor velocidad y mayor energía cinética.
Si la energía cinética es un componente de la aceleración gravitatoria, la energía potencial gravitatoria también se verá afectada. En otras palabras, si la fuerza gravitatoria es mayor con el movimiento, la suma de todas las fuerzas puntuales en la trayectoria de caída libre de un cuerpo que constituyen la energía potencial gravitatoria también será mayor.
En definitiva, la energía mecánica es mayor con la Ley de la Gravedad Global que en la Relatividad General de Einstein que, a su vez, es mayor que en la Física Clásica de Newton.
Si bien, en relación al párrafo anterior es necesario realizar dos precisiones conceptuales.
No me puedo imaginar cómo afecta la distorsión del espacio-tiempo a la energía potencial en la Relatividad General.
La energía mecánica en la Física Global depende de la velocidad escalar de la masa respecto al Éter Global (gravitacional - cinético - masa) y su velocidad vectorial respecto al campo de gravedad; en consecuencia, no es constante.
El libro Física y Dinámica Global describe las fuerzas de acción y reacción en el movimiento de caída libre y se estudia la energía cinética y la energía potencial gravitatoria desde la perspectiva de los mecanismos del movimiento con la aportación de la Ley de la Gravedad Global.

* * *
