2.c.2) Space-time relation and velocity
The concept of space-time continuum arises when the definition of velocity suffers a reversal. Velocity is no longer the relationship between space and time; a maximum appears conventionally. Therefore, space and time start to depend on each other so that the speed of light keeps constant. This interdependent concept configures the nature of space-time in the Theory of Relativity.
Nonetheless, let us go bit by bit.
Relativity of time
The law of relativity of time comes from the interpretation given to Michelson-Morley experiment. If one travels two different distances simultaneously and with the same speed, the only option not to get lost entirely is to make time relative.
In the Theory of Relativity, the time t0 measured by an observer with a clock at rest for events that take place in the same spot is the proper time of the interval between events.
A typical example found in books, meant to explain the concept of space-time and the so-called dilation of time, consists of an optical clock on a spacecraft and another on Earth. We will discuss it below.
From the Earth, an observer would see that the ray of light from the optical clock goes in zigzag due to the movement of the spacecraft, while the clock on Earth would go directly from top to bottom.
Consequently, given the difference in the distance traveled by light and its constant speed, we must conclude that time changes for each observer. The dilation of time will be:
t = t0 * (1 - v²/c²)-½
Obviously, it is easy to generalize the thought experiment dealing with the structure of space-time to common clocks, and the dilation of time is, of course, super-proven thoughtfully. As a specific book says “…this response is confirmed by detailed calculations regarding what happens to common clocks in motion, seen from the Earth.”
The concept of relativity of time has various implications. A prominent example is that simultaneity also ends up being relative, and even the principle of conservation of energy evolves to maintain its validity. The book Experiments of Global Physics proposes various scientific experiments about the measurement of time; in particular, the experiment Train of the Abrujuela, which deals with the problem of simultaneity.
Regarding the question of time travel, dilation of time does not run back for any observer, though some quantum-relativistic scientists may try to achieve the contrary.
The paradox of the twins –optical clocks, normal ones or people– confuses the philosophy of space-time because of the problem of which observer is to the right. The dilation of time effect of the observer on Earth respect to the clock on the spacecraft would be entirely symmetric to the effect on the observer on the spacecraft from the clock on Earth.
General Relativity gives an imaginary solution to the paradox of the twins. Relativistic mechanics tells us that accelerated reference systems are non-inertial, and one would have to take into account the various accelerations and decelerations of the spacecraft. Because of these successive accelerations, the spacecraft has been in different inertial reference systems.
In this book, there is a page dedicated to the Paradox of the twins, where we explain that it does not have a solution, nor can it have one in relativistic physics.
Another way of deducing the supposed relativistic nature of space-time –a little more complicated because one needs to master Pythagoras theorem– is using Lorentz equations. These were like a mathematical game until Albert Einstein discovered their true meaning.
Lorentz equations substitute Galileo transformations so that the two postulates of Special Relativity are valid: the expression of physical laws will not change, and the speed of light will be the same for all observers.
Relativity of Space
The measurements of space may be relative any point, but a universal origin of space does not exist, or at least it is unknown.
Here the principle that all motion is relative appears again, but the relativistic relation of space and time does not refer to this fact, but rather to the contraction of space according to whether we measure the speed in one reference system or another.
In other words, a meter does not always imply the same distance; it depends on the observer and his relative velocity. The only thing that remains constant with the philosophy of the curvature of space and time is the speed of light or space-time relation.
This concept of relativity comes from the thought experiment of the optical clock when the ray of light is moving in the direction of the spacecraft; as well as, of course, the orthodox interpretation of the Michelson-Morley experiment.
The hypothesis of contraction of objects in motion is the Fitzgerald-Lorentz contraction, and it is similar and complementary to that of time. It depends on the space-time axis that we consider affected in the relative motion between the frames of reference, the one for time, or the one for space.
If only the alteration of space is considered:
L0 = x'2 - x'1
L = L0 / γThe relation of transformation still depends on γ, specifically, on its inverse. If it affects both axes, the mathematical formulae would simply become more complex, but the reasoning behind them would be similar.
The book Global Dynamics analyses in depth the motion of light in the new theory of everything. The Global Physics assumes a philosophy of absolute time and space.
Let us see a detailed explanation of the thought example-experiment of the optical clock in Theory of Relativity.
In this case, description of physical reality is, in our opinion, mistaken, because it implicitly incorporates inertia of light. The thought experiment caught our attention because a concept often discussed in this area is precisely that of inertial and non-inertial systems.
Another very intriguing aspect, and quite frightening, is that if the academia is using a thought experiment as an example, it must be because it does not have a more appropriate physical experiment. We would say that reality is not how it seems in the following thought experiment:
Unreal or contradictory hypotheses
“On a spaceship, a ray of light is shot out in a perpendicular direction to that of the ship. The ray hits a mirror and goes back to its initial point; an observer on the spacecraft will see both the outward and return journeys in a perpendicular direction to the movement of the ship. On the contrary, because the spacecraft is moving at great speed, an observer on Earth would see the movement of the light ray as a zigzag. In other words, the distance traveled will be greater for him than for the observer on the ship”.
We believe the speed of light is additive to that of Earth gravity field, but not to that of a train; in space, the same would occur concerning its gravity field –LUM aether–, but not to the speed of a spacecraft.
The rest is easy. If one admits the constancy of the speed of light and assumes the inertia in its first trajectory and the return journey, the distance will be larger on the spacecraft than in the Earth. Then, the only possible solution is to make time relative and to invent relativistic space-time.
Here we come across a rectangular triangle again; time will have dilated enough that, with a constant velocity, the length corresponding to the initial distance (a) will be equal to the hypotenuse (c). In other words, the ratio of temporal dilation will be the inverse of the cosine of the angle formed between both these sides (c/a), which corresponds to the first auxiliary variable in the Lorentz equations. It means it will also be equal to the inverse of the square root of (1 - b²/c²)²), which deduces from Pythagoras’ theorem and coincides with the second auxiliary variable from the Lorentz transformations.
Thought experiment (FLAWED) 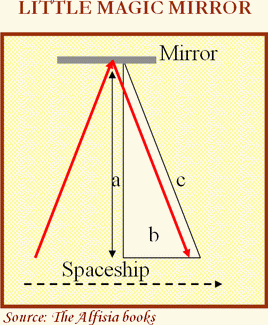
Honestly, one almost wants to ask “Oh magic mirror, which is the nicer theory?”
Moreover, we are afraid that if we had more observers or mirrors, we would obtain more triangles with a common side, and then we would have to make relative what is relative. Imagine the curvature of space-time that we could obtain with a pair of huge hexagons.
Other examples that we have seen in books on Relativity about crossing a river with a boat taking into account the movement of the water are similar.
