2.c.2.a) Pythagoras’ theorem and Einstein’s Relativity
The Theory of Special Relativity is associated with great mathematical complexity, but we believe the complexity is conceptual rather than mathematical, as it derives from the application of Pythagoras’ theorem.
-
One must not forget that we express concepts by means of words, and our brain has some meanings extremely ingrained, as they are very basic in a vital sense. Words like space and time are preconceptions recorded deep in our mind.
Of course, at the same time, not only references to space are relative, but space itself is too.
There is an explanation regarding the relativity of the perception of time by living beings, including twins; or the subjective relativity of time. Also, love appeared in the middle of it, We suppose that it was more convincing. Who would dare deny that…?
Because this perception or subjective reality does indeed exist, they ended up accepting a scientific model, which states that if two objects are moving away from each other at the speed of light, the velocity at which they are separating will still be the speed of light, as in the experiment of the antipodal photons.
An additional element is that everything is relative; and when it is convenient because something does not quite fit, one can say “Well, actually the matter is a lot more complex, but we were simplifying it implicitly, for… you.”
In any case, if required they just go back to tensors in the formulae of General Relativity and… lights out!
Why do they not explain that relativity of time means an asymptotic conversion of the speed of light so that it cannot exceed c and that it merely deduces from Pythagoras’ theorem? Alternatively, even simpler, that the rate for the folding and unfolding of time is the inverse of the cosine of corresponding sides of the rectangular triangle.
Discovery in Greece of Pythagoras’ theorem
In case one consider relativistic physics complex, let us do an exercise and try to imagine how it must have been discovered in its time, and what Pythagoras’ theorem involves of (assuming that they knew of the postal envelope and a bit of mechanics).
The trick entailed thinking of the envelope as open and closed simultaneously as if we were dealing with a quantum envelope. We look at the geometric curvature of the flap when it folds over inside the big square B (side=b), unfolds, expands or comes out and forms the small square A (side=a)
One can easily observe that the area of B is double the area of A. Then, as the area of B is b² and that of A is a², we find that [b² = a² + a²], and when we take the square root of this, we obtain Pythagoras’ Theorem.
Area of A = a² = b² / 2
When teaching children how to find the area of a square knowing its diagonal, they usually say one must calculate the length of the side using Pythagoras’ theorem and then, square it, instead of saying that it is equal to the diagonal squared divided by two.
Pythagoras theorem 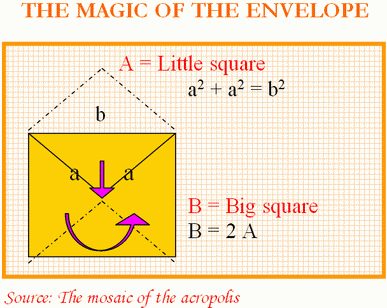
A concrete application of Pythagoras’ Theorem to Special Relativity is in the figure of the thought experiment Unreal or contradictory hypotheses.
This thought experiment shows the rectangular triangle that comes from different perspectives of two observers, plus the implicit idea that light conserves the inertia of the spacecraft, but only a hypothetical observer perceives that.
The figure is similar to the assumption above when talking about the element of the relativity of time; from where the temporal difference was:
t = t0 /(1 - v²/c²)½
Discovery in America of Special Relativity
Effectively, a small calculation based on the modern Pythagoras’ theorem, where the legs and the hypotenuse are distances traveled by the light and by the object in relative motion, seen from different imaginary observers and conveniently mixed, gives us the result previously shown.
In order to help assimilate the above, we show the following equations, which allow getting an immediate idea of where this Pythagorean time is going. Also, bearing in mind the difficulty in its recognition, and because it has terrified the little neurons of half the world, it could be a phantasmagorical time.
The idea is to normalize the hypotenuse of the triangle as c or the speed of light. If the velocity u and c are identical –because they are those of light– while v is that of the spacecraft, we will find that the dilation of time must be proportional to the inverse of the cosine of the angle α.
Analytical deduction Pythagoras’ Theorem u² = c² - v² Normalization c² u² / c² = 1 - v²/c² Square root and we get Cos α = u / c = (1 - v²/c²)½ Find c c = u * (1 - v²/c²)-½ Substitute auxiliary Lorentz
constant γc = u * γ If light incorporates the inertia for an observer, we would have to conclude that he would think that we had the typical case of inertial systems with additive velocities, unless it was an observer of the zigzag but unaware of its meaning.
As we will see further on, he would not be far off from the vision of reality that consciously is proposed!
Subsequently, the Lorentz transformations are perfect to ward off the ghost of Pythagoras. However, note the similarities of the two forms that the cos a takes with the two auxiliary constants of the equations.
One could say that Pythagoras’ theorem is a particular application of the specific case of the Thales theorem when a straight angle exists.
It is also widely known that the fundamental theorem in trigonometry, sine squared plus cosine squared equal to one, is an elemental implication of Pythagoras’ theorem. Both the quantifications of sine and cosine are by definition by considering the hypotenuse equal to unity. In other words, they would mean the number of hypotenuses in the adjacent leg or opposite leg to the angle in question.
At least traveling back in time is not possible. Thank goodness, because it would be a supreme act of boldness. What it is not explained very well is how –after a lapse of relative time– one goes back to regular time. We suspect we might have to tug on the tensions of General Relativity!
The cooktop that could appear with time games is an apotheosis. Ovens that are simultaneous for intelligent observers but that are asynchronous for the other observers, stretching distances, geometric effects stimulating the imagination, etc.
