II.c.2.a) Teorema de Pitágoras e a Relatividade de Einstein
À Teoria da Relatividade Especial associa-se uma grande complexidade matemática, mas penso que a complexidade é muito mais conceptual do que matemática, já que basicamente consiste na aplicação do teorema de Pitágoras.
-
Não há que esquecer que os conceitos se expressam através de palavras e o nosso cérebro tem muito enraizados alguns significados por serem muito básicos em sentido vital. Palavras como espaço e tempo confirmam pré-conceitos gravados a muito baixo nível ou muito profundamente no nosso cérebro.
Claro, de passagem, não só se relativizam as referências do espaço como também o próprio espaço.
Como não era suficiente tudo isto, foi necessário acrescentar uma explicação com a ideia da relatividade da percepção do tempo pelos seres vivos, incluindo gêmeos; ou, se se preferir, a relatividade do tempo subjetivo. Até se meteu o amor pelo meio, suponho que para que fosse mais convincente. Vamos ver quem nega que...!
Ao existir efetivamente essa percepção ou essa realidade subjetiva, acabou por aceitar-se um modelo científico que diz que se dois objetos se afastam cada um à velocidade da luz, a velocidade a que se separam continua a ser a da luz, como na experiência dos fótons antípodos.
Um elemento adicional é que tudo é muito relativo e quando interessa, porque alguma coisa não encaixa, pode dizer-se: "Efetivamente o tema é muito mais complexo, mas estávamos fazendo uma simplificação implícita para... ti."
Além disso, em caso de necessidade remetem-te para os tensores das fórmulas a Relatividade Geral e... apagou-se a luz!
Por que não se explica que a relatividade do tempo significa uma conversão assintótica da velocidade da luz para que não ultrapasse c e que se deduz simplesmente do teorema de Pitágoras? Ou ainda mais simples, que a razão da dobra temporal ou desdobramento temporal é o inverso do cosseno dos lados correspondentes do triângulo retângulo. Refiro-me à razão ou proporção matemática, não à razão lógica, salvo que a primeira implique a segunda.
Descoberta na Grécia do teorema de Pitágoras
Se se considera complicada a física relativista, vamos fazer um exercício de como se deve ter descoberto na sua época e em que consiste o teorema de Pitágoras, supondo que conhecesse o envelope de enviar correio e um pouco de mecânica.
O truque consiste em pensar que o envelope está aberto e fechado ao mesmo tempo, como se se tratasse de um envelope quântico, e em reparar na curvatura geométrica da dobra ao girar dentro do quadrado grande B (lado=b), desdobrar-se, expandir-se ou sair para formar o quadrado pequeno A (lado=a)
Como se pode observar com facilidade, a área de B é o dobro que a de A. então, como a área de B é b² e a de A é a², temos que b² = a² + a²] e calculando a raiz quadrada obtemos o teorema de Pitágoras.
Área de A = a² = b² / 2
Uma curiosidade matemática muito comum nos colégios, desta vez com o próprio teorema de Pitágoras e não relacionada com a Teoria da Relatividade de Einstein, é quando ensinam que para calcular a área de um quadrado sabendo a sua diagonal, dizem que se tem que calcular o lado com o teorema de Pitágoras e depois elevado ao quadrado; em vez de dizer que é igual à diagonal ao quadrado dividido por dois.
Uma aplicação concreta do teorema de Pitágoras à Relatividade Especial está incluída na figura da experiência mental de Hipóteses irreais ou contraditórias.
No referido exemplo mostra-se o triângulo retângulo que se formaria pela diferente perspectiva de dois observadores e indica-se a ideia implícita de que a luz conserva a inércia da nave espacial, mas apenas um hipotético observador percebe a questão...
Teorema de Pitágoras 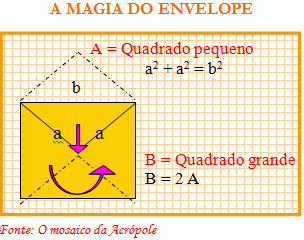
A citada figura é totalmente semelhante ao comentado ao falar do elemento da relatividade do tempo, de onde se deduziu que a diferença temporal podia calcular-se facilmente, sendo:
t = t0 /(1 - v²/c²)½
Descoberta na América da Relatividade Especial
Efetivamente, um pequeno cálculo baseado no moderno teorema de Pitágoras, onde os catetos e a hipotenusa são espaços percorridos pela luz e pelo objeto em movimento relativo vistos por distintos observadores imaginários e convenientemente misturados, dá-nos o resultado anteriormente mostrado.
Para facilitar a assimilação do que dissemos anteriormente, mostram-se as seguintes equações que permitem ter uma ideia imediata de qual é a tendência do tempo pitagórico e que, pela dificuldade em entendê-lo e reconhece-lo e por ter aterrados os neurônios de meio mundo, poderia expressar-se como tempo fantasmagórico.
Trata-se de normalizar a hipotenusa do triângulo por c ou velocidade da luz. Se a velocidade u e c são iguais porque são as da luz, enquanto que v é a da nave espacial, teremos que a dilatação do tempo deverá ser proporcional ao inverso do cosseno do ângulo α.
Dedução analítica Teorema de Pitágoras u² = c² - v² Normalização c² u² / c² = 1 - v²/c² Raiz quadrada e fica Cos α = u / c = (1 - v²/c²)½ Despejar c c = u * (1 - v²/c²)-½ Substituir constante auxiliar γ
de Lorenzc = u * γ Se a luz incorporasse a inércia para um observador haveria de concluir que ele pensaria que nos encontraríamos perante o típico caso de sistemas inerciais com velocidade aditivas, salvo que fosse um observador do ziguezague mas inconsciente do seu significado.
Como veremos mais à frente, não estaria muito longe da visão da realidade que conscientemente se propõe!
Depois introduzem-se as transformações de Lorentz para afastar o fantasma de Pitágoras. Não obstante, note-se a semelhança das duas formas que toma o Cos α com as duas constantes auxiliares das referidas equações.
E já agora, poderia dizer-se que o teorema de Pitágoras é uma aplicação particular do caso concreto do teorema de Tales quando existe um ângulo reto; enfim, tal para tal.
Também é sobejamente conhecido que o teorema fundamental da trigonometria, seno vezes seno mais cosseno ao quadrado igual a um, é uma implicação elementar do teorema de Pitágoras; uma vez que tanto a quantificação do seno como do cosseno se realiza por definição tomando a hipotenusa como unidade, ou seja, o número de hipotenusas no cateto contíguo ou cateto oposto ao ângulo em questão.
Pelo menos, diz-se que a viagem no tempo para trás não é possível. Menos mal, porque seria um atrevimento supremo. O que não explicam muito bem é como, depois de um lapso de tempo relativo, se volta ao tempo normal. Suspeito que será necessário recorrer às tensões da Relatividade Geral!
A confusão que se pode armar com os jogos com o tempo é apoteótico, acontecimentos simultâneos para observadores inteligentes que não são simultâneos para outro tipo de observadores, espaços que se alargam, efeitos geométricos que estimulam a imaginação, etc.
