3.b) Análisis preliminar - Correlación entre la escala Wechsler y Stanford-Binet
La primera sorpresa es la observación de las bajas correlaciones, no ya entre las variables M y P con las H sino también entre las propias H, tanto entre la escala Wechsler y Stanford-Binet como entre variables de la misma escala.
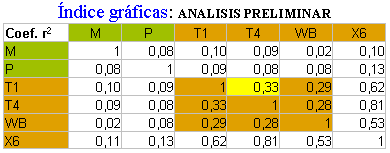
Cuadro estadístico de correlación en el análisis preliminar entre los cocientes de inteligencia de los padres y las madres con los CI de los hijos. Este cuadro estadístico ayuda a comprender las dificultades intrínsecas al modelo original, las razones para su reformulación e incluso la conveniencia de efectuar una simulación que confirme la bondad del modelo.
El coeficiente r²= 0,33 es el mayor entre las variables H, con esta perspectiva parece difícil imaginar que se puedan obtener correlaciones importantes entre los hijos y sus padres y madres.
escala Wechsler y Stanford-Binet
Al principio, todavía no había pensado en la agrupación de valores citada con anterioridad y, a la vista de estas correlaciones, pensé en sustituir los valores considerados muy dispares por sus medias, pero la correlación de las diferentes variables de las escalas Wechsler y Stanford-Binet seguía siendo realmente penosa.
Estas apreciaciones sobre la baja o no muy alta correlación entre las variables H (escala Wechsler, Stanford-Binet y habilidades mentales primarias) hacen pensar que las mediciones efectuadas no son muy homogéneas, puesto que parece que está aceptado generalmente que el CI de las personas permanece más o menos estable a partir de los 6 años.
Vistas las diferencias de las medias de las variables utilizadas, decidí estandarizarlas para un cálculo adecuado de las variables X3 y X6. Esta forma de calcular las medias es necesaria para evitar distorsiones y no plantea ningún problema adicional, teniendo en cuenta que no se pretende estudiar la evolución o aumento generacional de los CI, porque se considera un hecho probado y aceptado, aunque se ofrezcan diferentes explicaciones al respecto. En nuestro caso, los datos arrojan una media de las diferentes variables de los hijos un 10% superior a la media de las de los padres y madres.
Una consecuencia de la falta de precisión de las mediciones de los CI es la imposibilidad de seleccionar el 50% de la muestra de forma discrecional, para aislar los casos en que supuestamente domina el gen o cromosoma de menor potencial de acuerdo con lo señalado en el modelo estadístico propuesto inicialmente.
Es como si tuviésemos varios retratos robots de cada hijo que, en ocasiones, no se parecen en nada, pero que, en conjunto, quizás nos permitan una imagen relativamente nítida de la persona.
Otros factores que podían coadyuvar a la citada imposibilidad son la característica multifuncional del intelecto humano y que, como el propio modelo recoge, el CI del hijo pueda ser inferior al más pequeño de los progenitores por no encontrarse éste enteramente incluido en el mayor. Más adelante volveremos sobre este aspecto.
Como he señalado, este análisis preliminar me ha permitido conocer la dificultad de conseguir unos resultados satisfactorios y que es mejor utilizar los valores originales ya que su tratamiento, aunque objetivo, no mejora los resultados obtenidos de forma significativa.
También se han utilizado variables centradas, es decir, una con limitación de un 10% de la diferencia respecto a la media (T1-d) y las variables X3 y X6 que son los valores medios de tres y seis variables respectivamente. Como es lógico y se verá posteriormente, la variable X6 ofrece mejores resultados por ser una variable que responde, sin duda, mejor a la realidad por ser media de 6 variables observadas. (una de la escala Wechsler, 4 del test de Stanford-Binet y una del test de inteligencia de habilidades mentales primarias)
La solución vendrá con la reformulación del modelo y algo de imaginación.
