II.c.2.a) Théorème de Pythagore et Relativité d’Einstein
La Théorie de la Relativité Restreinte est associée à une grande complexité mathématique mais je pense que la complexité est plus conceptuelle que mathématique vu que cette théorie se base essentiellement sur l’application du théorème de Pythagore.
La complexité comme une excuse
Il ne faut pas oublier que les concepts sont exprimés par des mots et certains d’entre eux sont enracinés dans notre cerveau comme ayant un sens basique et vital. Des mots comme espace ou temps font partie de ces préconcepts gravés à bas niveau ou très profondément dans notre cerveau.
Bien sûr, en passant, non seulement les références de l’espace sont relativisées mais aussi l’espace lui-même.
Comme si cela ne suffisait pas, il a été nécessaire d’ajouter une explication avec l’idée de la relativité de la perception du temps pour les êtres vivants, y compris les jumeaux, ou si l’on préfère, la relativité du temps subjectif. Jusqu’à l’amour a été impliqué, à mon avis, pour que l’idée soit plus convaincante.
Cette perception ou réalité subjective en existant effectivement, a fini par accepter un modèle scientifique disant que si deux objets s’éloignent l’un de l’autre à la vitesse de la lumière, la vitesse qui les sépare continue d’être celle de la lumière, comme dans l’expérience des photons antipodes.
De plus, tout est très relatif et quand on s’y intéresse, si un élément ne colle pas, on peut dire : « Bon, en effet, le thème est bien plus complexe mais nous faisons une simplification implicite pour… toi. »
En plus, en cas de besoin, ils te renvoient aux tenseurs des formules la Relativité Générale… et le rideau se baisse !
Pourquoi n’explique-t-on pas que la relativité du temps définit une conversion asymptotique de la vitesse de la lumière afin qu’elle ne dépasse pas c et qu’elle se déduise facilement du théorème de Pythagore ? Ou plus simplement encore que la raison du pli temporel ou son contraire est l’inverse du cosinus des côtés correspondants du triangle rectangle. Je me réfère à la raison mathématique et non pas à la raison logique, sauf que le premier est sensé impliquer la seconde.
Découverte du théorème de Pythagore en Grèce
Au cas où la physique relativiste serait considérée comme compliquée, nous allons faire l’exercice de : « Comment a pu être découvert le théorème de Pythagore à son époque et, en supposant que l’enveloppe et quelques notion des mathématique étaient connues ? »
Il suffit de penser que l’enveloppe était ouverte et fermée en même temps, comme s’il s’agissait d’une enveloppe quantique, et que, en se concentrant sur la courbure géométrique du rabat en le retournant dans le grand cadre B (côté=B), se déplier, s’épandre ou sortir pour former le petit cadre A (côté=a)
Comme on peut facilement l’observer, l’aire de B est le double de celle de A. Donc, comme l’aire de B est b² et celle de A est a², on a que [b² = a² + a²] et, en sortant la racine carré, on obtient le théorème de Pythagore :
Area de A = a² = b² / 2
Une curiosité mathématique très commune dans les collèges, cette fois avec le théorème de Pythagore lui-même, sans lien avec la Théorie de la Relativité d’Einstein, ressort quand ils enseignent que pour calculer l’aire d’un carré en connaissant sa diagonale, il faut calculer le côté avec le théorème de Pythagore et qu’ensuite, il faut l’élever au carré. Tout cela au lieu de dire c’est égal à la diagonale au carré divisée par deux.
Théorème de Pythagore 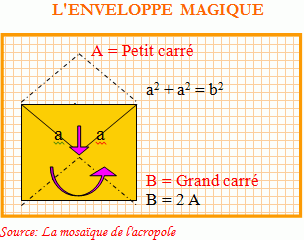
Cette application concrète du théorème de Pythagore à la Relativité Restreinte est reprise dans la figure de l’expérience mentale des Hypothèses irréelles ou contradictoires.
Dans cet exemple, on montre le triangle rectangle qui serait formé par la différence de perspective de deux observateurs et on indique l’idée implicite de la conservation de l’inertie par la lumière de la navette spatiale, mais seul un hypothétique observateur perçoit le sujet…
Cette figure est totalement semblable au supposé commentaire en parlant de l’élément de la relativité du temps, d’où l’on peut déduire que la différence temporelle pourrait facilement être calculée :
t = t0 /(1 - v²/c²)½
Découverte de la Relativité Restreinte aux Etats-Unis
En effet, un petit calcul basé sur le récent théorème de Pythagore, où les côtés et l’hypoténuse sont des espaces parcourus par la lumière et par l’objet en mouvement relatif vus par différents observateurs imaginaires et convenablement mélangés nous donne le résultat précédemment montré.
Pour faciliter l’assimilation de ce qui précède, les équations suivantes sont montrées afin de se faire immédiatement une idée de la direction de tir du temps pythagorique et, vu la difficulté soulevée pour les comprendre et les reconnaitre, vu la terreur qui affecte les petites neurones du monde du milieu, on pourrait exprimer le temps comme une entité fantasmagorique.
Il s’agit de normaliser l’hypoténuse du triangle par c (vitesse de la lumière). Si la vitesse u et c sont égales parce qu’elles sont celles de la lumière, alors que v est celle de la navette spatiale, nous obtiendrons que la dilatation du temps devra être proportionnelle à l’inverse du cosinus de l’angle α.
Déduction analytique Théorème de Pythagore u² = c² - v² Normalisation c² u² / c² = 1 - v²/c² Racine carrée y reste Cos α = u / c = (1 - v²/c²)½ Dégager c c = u * (1 - v²/c²)-½ Substituer constante auxiliaire γ
de Lorenzc = u * γ Si la lumière incorporait l’inertie, pour un observateur, il faudrait conclure qu’il penserait que nous nous trouvons devant le cas typique des systèmes inertiels aux vitesses additives, sauf qu’il s’agit d’un observateur du zigzag mais inconscient de sa signification.
Comme on le verra plus loin, il ne serait pas très loin de la vision de la réalité qu’il propose consciemment.
Ensuite les transformations de Lorentz ont été introduites pour éloigner le fantôme de Pythagore. Notez cependant la similitude des deux formes prises par Cos α avec les deux constantes auxiliaires de ces équations.
Tant que nous y sommes, on pourrait dire que le théorème de Pythagore est cas particuliers du cas concret du théorème de Thales quand il existe un angle droit.
Il également bien connu que le théorème fondamental de la trigonométrie, sinus au carré plus cosinus au carré égale un, est une implication élémentaire du théorème de Pythagore, vu que la quantification du sinus et du cosinus est par définition réalisée en prenant l'hypoténuse comme unité, c'est-à-dire la valeur de l'hypoténuse du côté contigu ou côté opposé sur l'angle en question.
Au moins, ils disent que le voyage dans le temps (vers le passé) n’est pas possible. Heureusement car ce serait l’audace suprême. Ce qu’ils n’expliquent pas bien, c’est comment, après un lapsus de temps relatif, on revient à un temps normal. Je crains qu’il ne faille tirer les tensions de la Relativité Générale !
Le foin qui s’est créé autour de joint du temps est sensationnel, évènements simultanés pour observateurs intelligents qui ne sont pas simultanés pour d’autre type d’observateurs, espaces qui s’épandent, effets géométriques qui stimulent l’imagination, etc.
