4.b.2. Curvatura della luce nell’effetto delle lenti gravitazionali
La predizione sul comportamento delle stelle come lenti gravitazionali nella curvatura della luce è la prima delle tre famose predizioni della Relatività Generale di Einstein e fu molto famosa per il ritardo nella sua conferma sperimentale fino all’eclisse solare del 1919.
Influisce inoltre sulla fama di questa predizione la presupposizione di un effetto di lente d’ingrandimento gravitazionale facile da visualizzare e che la curvatura della luce predetta dall’effetto di lente gravitazionale e poi confermata era esattamente il doppio di quella che sarebbe risultata dall’applicazione del Principio di Gravitazione Universale di Newton.
Risulta curioso che il continuum spazio-tempo si stiri-dilati nella curvatura della luce per l’effetto di lenti gravitazionali nel fattore *2* rispetto a quanto previsto dal Principio di Gravitazione di Newton e nessuno sembri sapere quale ne sia la ragione fisica, soprattutto perché il numero è piuttosto semplice. Ovviamente, il rinvio alle equazioni di campo di Einstein è sistematico, ma tutto qui.
Cercando su Internet –vedi articolo bending Light su mathpages.com *– o chiedendo ad un amico che davvero ne sa qualcosa di matematica e geometria ellittica, questo dirà che una particella che passa vicino al Sole forma un’iperbole in quanto quest’ultimo funge da lente gravitazionale e che, in funzione della sua eccentricità, per valori molto piccoli di m rispetto a r0 e secondo la Legge di Gravitazione di Newton, l’angolo o curvatura totale della luce sarà uguale a:
α = 2 m /r0 = 0,875'' di arco
In cui m è la massa del Sole in unità geometriche –la massa moltiplicata per G o costante di gravitazione e divisa per la velocità della luce al quadrato– e r0 la distanza più vicina del raggio di luce al Sole.
Ricordando un po’ la geometria di un circolo, un giro intero ha 360º gradi, ogni grado ha 60' minuti ed ogni minuto 60'' secondi di arco.
Dunque l’angolo o curvatura della luce che provocherebbero le lenti gravitazionali nella Legge di Gravitazione Universale di Newton è direttamente proporzionale alla massa che crea il campo di gravità, essendo la forza centripeta direttamente proporzionale alla massa.
Sebbene un pianeta abbia massa, in Meccanica Classica non si prende in considerazione questa massa, perché si esercita una forza gravitazionale sul pianeta in funzione della sua massa gravitazionale; ma la forza per unità di massa gravitazionale rimarrebbe costante, anche se si prendesse in considerazione la massa cinetica secondo la Teoria della Relatività di Einstein –massa equivalente all’energia cinetica.
Dunque, in base alla Legge di Gravità Globale, c'è una forza addizionale, la seconda componente dell’atractis causa o effetto Merlin è dovuto alla velocità ed agisce sulla massa cinetica. La massa globale è la massa in riposo più la massa equivalente all’energia cinetica. Nel caso della luce la massa a riposo non esiste.
Nella sezione sulla Legge di Gravità Globale di questo libro è stato detto che questa legge dovrebbe venire espressa in termini di energia e non di massa, poiché l’interazione gravitazionale avviene per trasferimento fra l’energia del campo di gravità e l’energia elastica in forma di massa, massa cinetica o direttamente l’energia elettromagnetica.
Per calcolare la curvatura della luce nell’effetto di lenti gravitazionali sull’energia elettromagnetica, ci rimane solo da verificare che la seconda componente o forza di gravità addizionale derivata dalla velocità è uguale quantitativamente uguale alla prima componente.
Nel caso dell’energia elettromagnetica è intuitivamente semplice, perché il valore dell’energia cinetica della luce sarà uguale all’energia cinetica equivalente alla presunta massa equivalente.
Anello Einstein - NASA (Immagine di dominio pubblico)

Da un altro punto di vista, se la prima componente dell’atractis causa è dovuta alla velocità della propagazione della tensione longitudinale dell’Etere Globale e questa è uguale alla velocità della luce, siccome la seconda componente –effetto Merlin– è dovuta alla velocità della luce per il caso dell’energia elettromagnetica, le due componenti dell’atractis causa avranno lo stesso valore e la curvatura della luce per le lenti gravitazionali sarà il doppio di quella che otterremmo con la Legge di Gravitazione di Newton.
La spiegazione precedente della causa fisica dell’effetto di lenti gravitazionali o curvatura della luce è un riassunto di quanto detto nella sezione seconda di questo libro, e nelle sezioni sul movimento con simmetria totale e con simmetria radiale della gravità nel libro della Fisica et Dinamica Globale.
Ciò nonostante per gli amanti della matematica viene inclusa la seguente analisi quantitativa che, oltre ad avere un certo valore educativo, è in qualche modo comune alla Fisica Globale e alla Teoria della Relatività.
ANALISI QUANTITATIVA
Ho già detto che il concetto di massa relativista o l’incremento della massa con la velocità è un aspetto parzialmente corretto della Teoria della Relatività –se si introduce il sistema di riferimenti naturale per la velocità fisica e, di conseguenza, si mantiene nella Fisica Globale–, basato su quest’ultimo modello nella pura osservazione sperimentale e nei meccanismi del trasferimento energetico dell’interazione gravitazionale, in contrapposizione all’imposizione di assiomi matematici alla Fisica.
Detto altrimenti, non è necessario mantenere la Teoria della Relatività per accettare il suddetto incremento della massa fisica con la velocità.
La nota formula della massa globale che serve per dedurre l’energia cinetica in termini relativisti è la seguente:
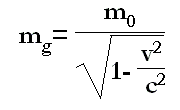
massa globale = massa in reposo + massa cinetica
[2.a] m = m0 /(1 - v²/c²)½
Oppure, in breve,
m = γ m0
Come indicato nella Teoria della Relatività di Einstein, l'energia cinetica è equivalente all'aumento della massa a riposo m0
Lo sviluppo in serie del teorema di Taylor della costante γ ci dà:
γ = 1+½ v²/c² +3/8 v4/c4+5/16 v6/c6+...
Energia cinetica = m0 [ ½ v²/c² +3/8 v4/c4+5/16 v6/c6+...]
A questi fini l’equazione rilevante della massa globale non deve contenere la semplificazione realizzata per l’energia cinetica classica nello sviluppo in serie del teorema di Taylor, poiché il secondo termine della parentesi diventa significativo per velocità dell’ordine della luce.
Da buon Einsaltro, ho chiesto qui a un amico mensista, che stava frequentando scienze esatte all’università e mi ha detto che non gliene fregava niente calcolare derivate terze, ovviamente lo capisco e siamo ancora amici.
A parte i simpatici aneddoti, nello sviluppo in serie del teorema Taylor sono validi solo i termini corrispondenti alle derivate della funzione, purché le derivate esistano, siano cioè diverse da zero. In generale, matematicamente nell’uguaglianza precedente si calcola l’ultimo termine valido in modo che vi appaiano i termini eliminati.
Nel nostro caso, se accumuliamo ( 1/8 v4/c4 ) al secondo termine raccoglieremo l’effetto residuale del resto di termini eliminati e ci rimarrà:
Energia cinetica = m0 [½ v²/c²+½ v4/c4]
Logicamente il primo termine della parentesi si può scartare per velocità basse o non planetarie, mentre il secondo termine si potrà scartare per quelle planetarie, ma non per velocità di ordine vicino a quello della luce ed ancora meno per la velocità simile al caso dell’effetto di lenti gravitazionali. Conseguentemente, in un’analisi generale vanno prese in considerazione tutte le possibilità del valore della velocità della massa fisica per determinare la forza di gravità totale.
E per di più, nell’equazione (2) della pagina in inglese di Mathpages.com ** sull’inerzia dell’energia appare l’utilizzo di questo stesso sviluppo in serie del teorema di Taylor.
(Velocità vicine alla luce)
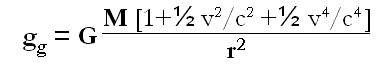
La dimostrazione della Relatività Generale che l’effetto delle lenti gravitazionali è il doppio rispetto alla Legge di Gravitazione di Newton è alquanto complessa; ma sembra che inevitabilmente si usi anche lo stesso sviluppo in serie del teorema di Taylor, come si può vedere nella pagina sulla curvatura della luce del sito di Mathpages.com, a cui ci siamo riferiti prima.
Al contrario, senza contare lo sviluppo in serie di Taylor, nella Fisica Globale, il calcolo non potrebbe essere più facile.
Quindi l’angolo della curvatura della luce per l’effetto delle lenti gravitazionali sarà il doppio di quello predetto dalla Legge di Gravitazione Universale della teoria di Newton, come già sapevamo per le famose osservazioni dell’eclisse di Sole del 1919, essendo l’arco 1,75''.
