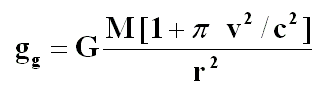3.b.3. L'énergie mécanique

La définition de l'énergie mécanique est la somme des énergies cinétiques et potentielles associées à une masse dans un champ gravitationnel. En l'absence d'autres forces l'énergie mécanique d'un corps en orbite reste constante.

Dans la Physique Moderne, l'énergie mécanique est un concept abstrait de somme d'énergie de nature mathématique, mais qui relie ou met en relation le mouvement en général avec le mouvement dû à la gravité.

Concept d'énergie mécanique cinétique comme propriété de la masse due à sa tendance à maintenir son état de mouvement et qui implique une plus grande résonnance de la masse ou synchronisation avec la vibration de la globine. Définition de l'énergie mécanique potentielle comme propriété d'une masse à se trouver en un point de la structure réticulaire de la matière, globine avec symétrie radiale ou champ gravitationnel. Dans le premier cas, on parle aussi d'énergie cinétique et dans le deuxième de l'énergie potentielle ou énergie gravitationnelle.

La raison qui fait que l'énergie mécanique est constante est conventionnelle ou dérivée du principe de conservation des énergies. Si le système est fermé, et si l'on considère seulement deux manifestations de l'énergie, la somme des deux doit être constante.

Avec la théorie de la gravitation de Newton, les orbites des planètes étaient expliquées et le principe d'égalité entre masse inertielle et masse gravitationnelle était maintenu. La masse dans les deux cas était une constante de proportionnalité entre la force appliquée et l'accélération résultante des corps. L'accélération de la gravité suit la loi de l'inverse des carrés par conséquence des propriétés élastiques de la globine.

La Théorie de la Relativité d'Einstein maintient le principe d'égalité entre masse inertielle et masse gravitationnelle, mais continue sans savoir ce qu’est la masse au-delà de la constante de proportionnalité. La masse augmente avec la vitesse relative, ceci dû au modèle mathématique utilisé, et cette augmentation implique une plus grande force pour produire la même accélération.

Par conséquent, avec la Théorie de la Relativité d'Einstein, l'énergie mécanique est plus grande que dans la Physique Classique de Newton, car l'énergie cinétique d'un objet en chute libre verticale sera plus grande à cause de l'augmentation de masse avec la vitesse.

En plus, curieusement comme la masse gravitationnelle semble avoir un comportement différent de celui de la mase inertielle, vu qu’une augmentation de la masse avec la vitesse n’altèrerait pas la force de gravitation par unité de masse, la Relativité Générale d'Einstein doit déformer l'espace pour pouvoir faire cadrer les orbites des planètes et leur précession anormale par rapport à la Loi de la Gravitation Universelle de Newton.

Comme dans la Relativité Générale d'Einstein la distorsion de l'espace suit la même règle, loi de gravitation de l'inverse des carrés, la gravité entière passe pour être un effet géométrique du continuum mathématique et les concepts intuitifs de la réalité physique se perdent encore plus.

Energie mécanique
(Image du domaine publique)

Vu que la loi qui gouverne l'élasticité de la globine est présente dans tous les types de relations physiques, à de nombreuses occasions, les calculs mathématiques des modèles imaginaires sont utiles pour des interprétations physiques assez éloignées de la réalité. Jusqu’ici, il semble que le sujet soit facile, très facile, si facile qu’il est facile de se tromper.

Pour la Mécanique Globale, la masse est formée de boucles de la structure matérielle de la globine ou filament de la structure réticulaire de Globus. Ainsi, le principe d'égalité de masse inertielle ou gravitationnelle doit être compris comme l'égal comportement inertiel ou gravitationnel de la masse physique, vu que la réalité physique pour la Mécanique Globale est unique et ne dépend pas des observateurs.

Formule de la Loi de la Gravité Globale
 

La Loi de la Gravité Globale apporte une seconde modification ou nuance à la Seconde Loi de Newton, Loi de la Force ou Loi Fondamentale de la Dynamique. Si Einstein a introduit une variation intrinsèque de la masse avec la vitesse et l'augmentation correspondante d'attraction gravitationnelle, la Loi de la Gravité Globale ajoute une variation additionnelle de la force d'attraction gravitationnelle due à la vitesse et distincte de celle induite par l'augmentation citée plus haut de la masse, bien qu’elle soit toutes deux des variations identiques en termes quantitatifs.

Dans ce cas, il se produira une augmentation de l'accélération gravitationnelle, qui sera directement proportionnelle à l'énergie cinétique comme on observe dans la Loi de la Gravité Globale. Avec cette modification de la Loi de la Gravitation Universelle de Newton, on explique la précession anormale des orbites des planètes sans altérer l'espace-temps.

Par conséquence, la nouvelle augmentation de la force de gravité produira une accélération plus forte, une vitesse plus grande et une énergie cinétique plus importante.

En d'autres termes, si l'énergie cinétique est une composante de l'accélération gravitationnelle, l'énergie potentielle gravitationnelle aussi se verra affectée. En d'autres termes, si la force de gravitation est plus grande avec le mouvement, la somme de toutes les forces ponctuelles dans la trajectoire de chute libre d'un corps qui constituent l'énergie potentielle gravitationnelle sera aussi plus grande.

Depuis une autre perspective, l'augmentation de l'énergie potentielle gravitationnelle est nécessaire pour maintenir l'énergie mécanique constante.

En définitive, l'énergie mécanique est plus grande dans la Loi de la Gravité Globale que dans la Théorie de la Relativité d'Einstein qui, à son tour est plus grande que dans la Physique Classique de Newton.

Dans le livre en ligne de la Dynamique Globale on étudie plus en détails l'énergie cinétique et l'énergie potentielle gravitationnelle depuis la perspective du mouvement avec l'apport de la Loi de la Gravité Globale.