2.b.1. The gravitational interaction and the gravitational force

Until the introduction of gravity and its gravitational force any of the reticules in structure of matter in the Euclidian space would have the same properties. It other words, globine would have a symmetry in every direction, global symmetry of super symmetry.

In the previous part on gravitational theory we saw the physical properties of the phases of matter that configure gravity, especially the introduction of radial symmetry and the additive tension in the longitudinal curvature of the globine.

As shown in the figures, the quoted super symmetry breaks in the gravitational field, because of the effect of mass when provoking a separation of filaments in gravity’s reticular structure. Besides the radial symmetry of the gravitational field, on the shown images we can recognize an up-and-below or respect to the horizontal axis symmetry, where the filaments in gravity’s reticular structure are convex towards the axis of symmetry.

In other words, the mass provokes an elastic tension in the gravitational field’s three-dimensional net when separating the filaments on one end, so that the interior of the lines are convex towards the mass or point with the biggest separation of the filaments or lines of elastic tension, provoking the vertical asymmetry of the heyelogic figure.

Regarding the gravitational force it is important to point out that there could be two different causes, one explaining the movement due to the classical gravitational force or force of gravity by Newton, and another elucidating the movement of the anomalous precision of the orbit of Mercury in replacement of the distortion of the space suggested by Einstein in his General Theory on Relativity.

The online book on the Law of Global Gravity will analyze the mentioned causes and their mathematical formulas by Newton's Law in the Universal Gravity with the incorporation of a correction by the Law on Global Gravity a propos the effect of the kinetic energy on the force of the gravitational attraction.

We will also leave the analysis of the characteristics of forces of gravity of atomic distances for another section.

Finally, we will dedicate another section to the topic related to the force of the gravitational interaction in the Law of Global Gravity book; it is about the characteristics of gravitational waves and the different definitions or concepts used to refer to them. Particularly, some ideas on the characteristics of longitudinal waves and on the speed of the transmission of the potential gravitational energy are included.

Now we will analyze one of the most relevant aspects of the gravitational interaction. The additive property of the tension of longitudinal curvature of globine or potential elastic energy that supports the gravitational force.

• The additive property of the gravitational force

  The longitudinal curvature, which provokes or supports the gravitational interaction, together with the characteristic of rigidity, causes the generation of elastic lines of tension in the filaments of gravity’s three-dimensional structure.

  The electromagnetic fields also possess the additive property of its potentials, as we will see later its material support is also the globine, but it would be about the transversal elasticity of its filaments. 

  The colors red and green in the three figures below on the gravitational force show the additive property of the elasticity of the longitudinal curvature as a linear relation, when summing up the vertical distances between the filaments; a greater approach to reality would be to sum up the distances in a semi-logarithmic scale because of the inverse-square law.

  Gravitational force
  Convexity towards the axis of symmetry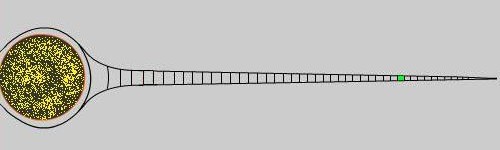 
  Radial Symmetry of gravitational force
  
  Additive property of gravitational force
  

  With the gravitational force based on a structure of elastic three-dimensional reticules, the characteristic of having additive tension is quite intuitive. However I consider opportune to underline two new aspects of the gravitational model:

  • We should not confuse the mathematical representation of a gravitational field by using lines of force of the field with the material filaments that support or allow the gravitational force.

  • The maximum separation of the filaments will be determined by the pure longitudinal elasticity of the edges of the three-dimensional reticules of the matter’s structure. In the figure, it would be a shorter distance than the diameter of the ball of mass, which at the same time would also be determined by the quoted reticular elasticity as we will see when talking about what the physical mass is and the fundamental particles with mass and stables.

  The rigidity of the phase matter of gravity’s structure will cause the convexity to decrease until very long distances in accordance to the attraction of the gravitational law with its inverse-square law.

  The curvature created in the filaments of the reticular composition of gravity or globine implies the existence of a potential elastic energy and it will have an asymptotic shape in the right part of the mentioned figure, related to the horizontal axis of symmetry. This elastic tension of the filaments is responsible for the multiple components of the force of gravitational attraction and the gravitational acceleration.