4.b.2. Light curve and gravitational lensing effect
Prediction about the behavior of stars as a gravitational lens in the light curve was the first of the three main predictions of General Relativity. Besides, it was very famous because of delay in its experimental confirmation, which did not take place until the 1919 solar eclipse.
Undoubtedly, the fame of this prediction is also due to the natural understanding of a magnifying glass effect, and that the light curve predicted and confirmed by gravitational lensing effect was exactly twice the value applying Newton’s Law of Universal Gravitation.
It is bizarre that space-time continuum is stretched-prolonged in the light curve because of gravitational lensing effect in factor *2* regarding what was foreseen by Newton’s Gravitational Law and no one seems to know its physical reason, especially when the number is quite round and straightforward. Of course, there are systematic references to Einstein’s field tensor equations, gravity being a geometric effect of space-time and energy involvement.
Searching the Web –see article bending Light en mathpages.com **– or asking any friend who knows something about mathematics and elliptic geometry, we will say that any particle which passes near the Sun describes a hyperbole. Because the Sun acts as a gravitational lens and that, depending on its eccentricity, for small values of m regarding r0 and according to Newton’s Gravitational Law, the angle or total light curve should be equal to:
α = 2 m /r0 = 0,875'' arc seconds
Where m is the mass of the Sun in geometric units –mass multiplied by G or Gravitational Constant and divided by the speed of light squared– and r0 is the closer distance of ray of light to the Sun.
To remind geometry of a circle, we will just say that there are 360 degrees in a full turn, 60' minutes in each grade and 60'' arc seconds in each minute.
Therefore, angle or light curve provoked by gravitational lensing in Newton’s Law of Universal Gravitation is directly proportional to the mass generated by the field of gravity, since centripetal force is directly proportional to the mass.
Even though a planet has mass, in Classical Mechanics its mass does not affect, since gravitational force on the planet is proportional to its gravitational mass. Therefore, force by a gravitational unit of mass will remain constant even if we take into account the kinetic mass –mass equivalent to kinetic energy.
Nevertheless, with the Law of Global Gravity, there is an additional force, the second component of the atractis causa or Merlin effect is due to velocity and operates on kinetic mass. Global mass is the mass at rest plus the mass equivalent to kinetic energy. In case of light, the mass at rest does not exist.
In section Law of Global Gravity, we mentioned we should express said the law in energy terms rather than in mass terms since gravitational interaction means an energy transfer between gravity field and the elastic energy in the form of mass, kinetic mass or electromagnetic energy.
In order to calculate light curve in gravitational lensing effect, we only have to verify that second component or additional force of gravity derived from speed is quantitatively equal to the first component.
Intuitively, it is simple, because light kinetic energy value will be equal to the supposed equivalent kinetic mass.
Einstein Ring - NASA (Public domain image)

From another point of view, the first component of the atractis causa is due to the propagation speed of the Global Aether’s longitudinal tension, and it is equal to the speed of light. Since second component –Merlin effect– is due to the speed of light for the case of electromagnetic energy, both components of the atractis causa will have the same value and light curve due to gravitational lenses will be twice the value we would obtain with Newton’s Gravitational Law.
Previous explanation of the physical cause of gravitational lensing effect is a summary of what we discussed in both the chapter of this book and sections on motion with super symmetry and gravity radial symmetry of the book Physics and Global Dynamics.
Nevertheless, for mathematics lovers we have included the following quantitative analysis, which has some educational value and, to some extent, it is common to Global Physics and General Relativity.
QUANTITATIVE ANALYSIS
We have previously mentioned relativistic mass or increase in mass due to velocity is a partially correct aspect of the Theory of Relativity –when it uses natural reference system– and, consequently, this concept remains in Global Physics. This new theory seats on pure experimental observation and theoretical energetic transfer mechanisms of gravitational interaction, in comparison with the imposition of mathematical axioms in Modern Physics.
In other words, there is no need for the Theory of Relativity to accept said the increase in physical mass.
The famous global mass formula used for inferring the kinetic energy in relativistic terms is the following one:
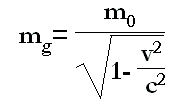
global mass = mass at rest + kinetic mass
[2.a] m = m0 /(1 - v²/c²)½
Alternatively, for short,
mg = γ m0
Where m is the mass or relativistic mass of the body, m0 is mass at rest and v the velocity.
As pointed out by the Theory of Relativity of Einstein, kinetic energy is equivalent to increase of the mass at rest m0
The result of the series expansion of Taylor’s theorem of constant γ is:
γ = 1+½ v²/c² +3/8 v4/c4+5/16 v6/c6+...
Kinetic energy = m0 [ ½ v²/c² +3/8 v4/c4+5/16 v6/c6+...]
To these effects, the relevant equation of global mass should not include the simplification made for classical kinetic energy in the series development of Taylor’s theorem, since the second term in the parenthesis becomes significant for speeds similar to the speed of light.
As a good Einsotro, at this point I asked a Mensa friend who was studying Exact Sciences at university. He answered that he did not feel like calculating third derivatives. I can understand him, of course, and even though he is still my friend.
Apart from amusing anecdotes, only the terms corresponding to function derivatives in the expansion of Taylor’s series are valid as long as said derivatives exist; in other words, as long as they are different from zero. In general, mathematically in the preceding equality, the last valid term calculus collects the eliminated terms.
In this case, if we accumulate ( 1/8 v4/c4 ) to the second term we will obtain the residual effect of the rest of eliminated terms, and the result will be:
Kinetic energy = m0 [½ v²/c²+½ v4/c4]
Obviously, the first term of the parenthesis can vanish with low or non-planetary speeds, while the second one will disappear with planetary velocities but not with speeds close to speed of light and, in no way, with similar velocities to light as in case of gravitational lensing effect. Consequently, within a general analysis, we should consider all possibilities the physical mass velocity to resolve total gravity force.
Furthermore, in equation (2) of webpage Mathpages.com ** about the inertia of energy we can find the use of this series development of Taylor’s theorem.
(Speeds similar to the speed of light)
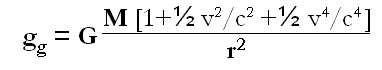
General Relativity proving gravitational lensing effect is twice than in Newton’s Gravitational Law is quite intricate. However, it inevitably uses same series development of Taylor’s theorem, as one may see on the Web page about the light curve of Mathpages.com.
On the other hand, without taking into account Taylor’s series development, the calculus cannot be accessible in Global Physics.
Therefore, angle due to gravitational lensing effect will be twice the one predicted by the Law of Universal Gravitation of Newton, as we already knew by famous observations of the 1919 solar eclipse and subsequent ones, being 1,75''arc seconds.
