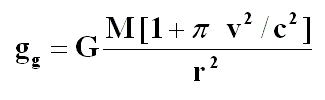3.b.3. Mechanical energy in Physics
In Modern Physics, the definition of mechanical energy is the sum of kinetic and potential energies related to a specific mass in a gravitational field. In the absence of other forces, the mechanical energy of a body in orbit remains constant.
Mechanical energy is an abstract concept or a sum of energies of a mathematical nature that connects causes of inertial motion with motion due to the force of gravity.
The reason why mechanical energy is constant is conventional and derived from the Principle of Energy Conservation. In a closed system and with only two energy manifestations, the sum of both of them should be constant.
Newton’s theory of gravitation explained planet orbits and outspread the principle of equality between inertial and gravitational mass. In both cases, the mass was a constant of proportionality between the applied force and the resulting acceleration of bodies. The acceleration of gravity follows the inverse-square law.
Einstein’s Theory of Relativity keeps the principle of equality between inertial and gravitational mass but still, does not know what mass is beyond a constant of proportionality. Mass does not increase with relative speed thanks to the mathematical model used, but it is multiplied by γ –in fact as if it would increase–, and such increase makes necessary a higher force with higher speed to generate the same acceleration.
In Einstein’s General Relativity mechanical energy is higher than in Newton’s Classical Physics since the kinetic energy of a body in a vertical free fall will be higher because mass increases with velocity.
However, according to observations, gravitational mass seems to have a different behavior from inertial mass. As an increase in mass with velocity does not alter the gravitational force by a unit of mass, Einstein’s General Relativity needs to distort space to adjust orbits of the planets and their anomalous precession regarding Newton’s Law of Universal Gravitation.
(Public domain image)

An additional problem generated by General Relativity is that, as space distortion follows the same law of the inverse-square whole gravity becomes a geometrical effect of the mathematical continuum and intuitive concepts of physical reality blur even more.
Since laws governing elasticity of the Global Aether are present in all type of physical relations –like the inverse-square law–, mathematical calculus of theoretical models on many occasions are useful with physical interpretations quite distant from reality. This topic even could seem so, so easy that is easy to get wrong.
For Global Mechanics, mass consists of loops of the filaments of gravitational, kinetic or Global Aether. Thus, the principle of equality between inertial and gravitational mass, besides being puzzling, it is not necessary anymore, because physical reality defines mass and not its behavior.
In Global Physics, the concept of kinetic energy is a property of mass associated with a tendency to keep its state of movement, which implies a higher mass resonance to conserve synchronization with the vibration of the Global Aether (gravitational - kinetic - mass).
Definition of potential energy is a property of the mass of being at a given point of the reticular structure of matter –Global Aether– with radial symmetry.
The Law of Global Gravity provides a second modification or nuance to Newton’s Second Law, Law of Force or Fundamental Law of Dynamics. If Einstein introduced an intrinsic variation of mass with velocity and the corresponding increase in gravitational attraction plus the space-time distortion, the Law of Global Gravity adds a variation in gravity force due to velocity, which is different from the correspondent mass increment, even though both variations are identical in quantitative terms.
In this case, an increase in gravitational acceleration, which would depend on kinetic energy –in particular, on the relationship between kinetic and global mass–, as observed in the Law of Global Gravity. This modification of Newton’s Law of Universal Gravitation explains the anomalous precession of orbits of the planets without altering space and time.
As a result, a new increase in the force of gravity will generate higher acceleration, higher speed, and higher kinetic energy.
In other words, if kinetic energy is a component of gravitational acceleration, gravitational potential energy will change. That is, if gravitational force increases with motion, the sum of all forces along the trajectory of the body’s free fall, which constitutes its gravitational potential energy, will also be higher.
In short, mechanical energy is higher in the Law of Global Gravity than in Einstein’s General Relativity, which, in turn, is higher than in Newton’s Classical Physics.
Nevertheless, it is required to make two conceptual clarifications regarding the previous paragraph.
We cannot imagine how distortion of space-time affects potential energy in General Relativity.
-
Mechanical energy in Global Physics depends on the scalar speed of the mass relative to Global Aether and vector velocity relative to gravity field; accordingly, it is not constant.
The book Physics and Global Dynamics describes the forces of action and reaction in the free fall movement and deals with both kinetic and gravitational potential energies from the viewpoint of the mechanisms of movement with the contribution of the Law of Global Gravity.

* * *